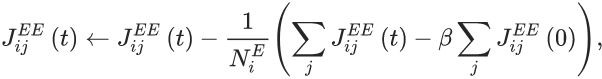I indeed think that you can probably avoid having user-defined functions or network operations, which would of course be preferable for full compatibility with all code generation targets (including support for the upcoming Brian2CUDA package). Your above code would be equivalent to simply using
eesyn.run_regularly('wee = wee - ...', dt=1*second)
though.
The problem here is that you need a way to sum over all weights – in a network operation, this is as simple as np.sum(eesyn.wee), but summing “in Brian equations” needs synapses.
From a quick look at the equation:
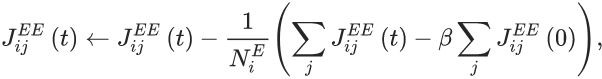
I gather that the \beta\sum_j\dots term is a constant (initial weights) that can be calculated before the simulation starts – for runtime that would be trivial, but it complicates the code a bit for standalone mode. The text also notes that it should only apply if the first term is bigger than the second term, but we can do this by thresholding with using clip(term, 0, inf). This leaves to calculate two values: the first is N_i^E, the number of non-zero weights a neuron receives – from a cursory look I wasn’t sure whether this is simply meant to count the number of incoming connections (which are already available as N_incoming), or whether the plasticity rule might make weights go to zero which should then not be included. I’ll assume the former for simplicity now. The second is \sum_j J_{ij}^{EE}, i.e. the sum of all weights to a neuron. We should be able to do this with a (summed) variable connecting the synapses to the neurons.
Here’s a simplified example showing how this can work:
from brian2 import *
neurons = NeuronGroup(10, '''total_weights : 1
initial_weights : 1 (constant)''')
# weights grow over time
growth = 0.1/second
beta = 1.08
synapses = Synapses(neurons, neurons, '''dw/dt = growth : 1 (clock-driven)
total_weights_post = w : 1 (summed)''')
# Somewhat hacky, but avoids that total_weights get updated every time step
synapses.summed_updaters['total_weights_post']._clock = Clock(dt = 1*second)
# Heterosynaptic plasticity
synapses.run_regularly('w -= clip(1/N_incoming*(total_weights_post - initial_weights_post), 0, inf)',
when='end', dt=1*second)
# Random connections with 0.2 probability
sources, targets = np.meshgrid(np.arange(len(neurons)), np.arange(len(neurons)))
sources, targets = sources.flatten(), targets.flatten()
pairs = np.random.rand(len(neurons)**2) < 0.2
synapses.connect(i=sources[pairs], j=targets[pairs])
# Random initial weights
weights = np.random.rand(sum(pairs))
synapses.w = weights
# Store initial total weight for each neuron
weights = [np.sum(weights[targets[pairs] == idx]) for idx in range(len(neurons))]
neurons.initial_weights = weights
mon = StateMonitor(synapses, 'w', record=np.arange(sum(pairs)))
run(1.5*second)
plt.plot(mon.t/ms, mon.w.T)
plt.show()
If you did not need standalone support, then this could be much simpler, e.g. connecting synapses could just use synapses.connect(p=0.2), setting random weights would use synapses.w = 'rand()', etc. For standalone support, all this randomness needs to be outside the generated code, since we need to access the initial weights before the actual simulation starts. I did not verify the results from this code thoroughly, but hopefully it gets you going! I think the metaplasticity thing should be straightforward with a run_regularly operation on the Synapses object (referring to a rate estimate in the neuron that gets updated for every spike as part of the reset) – but I might have missed something.