Change the neurons indices and firing times in SpikeGeneratorGroup?

Support
, ,
1

Description of problem

I’m trying to make the neuronal population fire according to precomputed sequences of firing. An encoding scheme produces those firing sequences. For instance, let’s assume i have 100 neurons

at t = 0 to 100 ms

[1, 20,12,23, ….. 67] —– fires at [0,1,2,5,6,11,…..]

at 100ms to 200ms

[2,1,55,3,8,90,1………] —–fires at [0,3,5,6,………..]

at 200ms to 300ms

………

It fires all neuronal populations at different times within a 100-ms period for the entire simulation, which lasts 10 seconds.

Minimal code to reproduce the problem

from brian2 import *
import os
import matplotlib.pyplot as plt
import numpy as np
taue = 5*ms
taui = 10*ms
Ee = 0*mV
Ei = -70*mV
os.environ['CC'] = 'gcc'
os.environ['CXX'] = 'g++'
dimension = 18
#t = 100
nGRFcells = 5
gamma = np.ones((nGRFcells, dimension))
Imax = np.max(info_matrix, axis = 0)
Imin = np.min(info_matrix , axis = 0)
print("I max", Imax)
print("I min", Imin)
iterations = 10
G = SpikeGeneratorGroup( dimension * nGRFcells, indicess, firing_t*ms)
# taken from Touboul_Brette_2008
eqs = """
dvm/dt = (g_l*(e_l - vm) + g_l*d_t*exp((vm-v_t)/d_t) + I_AMPA - I_NMDA + I_GABA +- w)/c_m : volt
dw/dt  = (a*(vm - e_l) - w)/tau_w : amp
I_AMPA = ge * (Ee - vm): amp
I_GABA = gi * (Ei - vm): amp
dge/dt = -ge / taue : siemens
dgi/dt = -gi / taui : siemens
I_NMDA: amp
"""
taum = 20*ms
taupre = 200*ms
taupost = 180*ms
gmax = .1
dApre = .0002
dApost = -dApre * taupre / taupost * 1.05
dApost *= gmax
dApre *= gmax

patterns = {
    "tonic spiking": {
        "c_m": 200 * pF,
        "g_l": 10 * nS,
        "e_l": -70.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": 2.0 * nS,
        "tau_w": 30.0 * ms,
        "b": 0.0 * pA,
        "v_r": -58.0 * mV,
        "i_stim": 500 * pA,
    },
    "adaptation": {
        "c_m": 200 * pF,
        "g_l": 12 * nS,
        "e_l": -70.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": 2.0 * nS,
        "tau_w": 300.0 * ms,
        "b": 60.0 * pA,
        "v_r": -58.0 * mV,
        "i_stim": 500 * pA,
    },
    "initial burst": {
        "c_m": 130 * pF,
        "g_l": 18 * nS,
        "e_l": -58.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": 4.0 * nS,
        "tau_w": 150.0 * ms,
        "b": 120.0 * pA,
        "v_r": -50.0 * mV,
        "i_stim": 400 * pA,
    },
    "regular bursting": {
        "c_m": 200 * pF,
        "g_l": 10 * nS,
        "e_l": -58.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": 2.0 * nS,
        "tau_w": 120.0 * ms,
        "b": 100.0 * pA,
        "v_r": -46.0 * mV,
        "i_stim": 210 * pA,
    },
    "delayed accelerating": {
        "c_m": 200 * pF,
        "g_l": 12 * nS,
        "e_l": -70.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": -10.0 * nS,
        "tau_w": 300.0 * ms,
        "b": 0.0 * pA,
        "v_r": -58.0 * mV,
        "i_stim": 300 * pA,
    },
    "delayed regular bursting": {
        "c_m": 100 * pF,
        "g_l": 10 * nS,
        "e_l": -65.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": -10.0 * nS,
        "tau_w": 90.0 * ms,
        "b": 30.0 * pA,
        "v_r": -47.0 * mV,
        "i_stim": 110 * pA,
    },
    "transient spiking": {
        "c_m": 100 * pF,
        "g_l": 10 * nS,
        "e_l": -65.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": 10.0 * nS,
        "tau_w": 90.0 * ms,
        "b": 100.0 * pA,
        "v_r": -47.0 * mV,
        "i_stim": 180 * pA,
    },
    "irregular spiking": {
        "c_m": 100 * pF,
        "g_l": 12 * nS,
        "e_l": -60.0 * mV,
        "v_t": -50.0 * mV,
        "d_t": 2.0 * mV,
        "a": -11.0 * nS,
        "tau_w": 130.0 * ms,
        "b": 30.0 * pA,
        "v_r": -48.0 * mV,
        "i_stim": 160 * pA,
    },
}
L1parameters = patterns["irregular spiking"]
L2parameters = patterns["adaptation"]
neuron = NeuronGroup(
    100,
    model=eqs,
    threshold="vm > 0*mV",
    reset="vm = v_r; w += b",
    method="euler",
    namespace=L1parameters,
)

neuron.vm = L1parameters["e_l"]
neuron.w = 0
# connecting the Cortical layer into output layer L4
#So = Synapses(G,neuron, on_pre='ge += 10*nS')
#So.connect(p=0.05)
S = Synapses(G, neuron,
             '''w1 : 1
                dApre/dt = -Apre / taupre : 1 (event-driven)
                dApost/dt = -Apost / taupost : 1 (event-driven)''',
             on_pre='''ge += w1 * siemens
                    Apre += dApre
                    w1 = clip(w1 + Apost, 0, gmax)''',
             on_post='''Apost += dApost
                     w1 = clip(w1 + Apre, 0, gmax)''',
             )
S.connect(p = 0.05)
S.w1 = '0.0001* rand()'
s = []
L1_mon = SpikeMonitor(neuron)
spike_mon = SpikeMonitor(G)
w_mon = StateMonitor(S, 'w1', record=[0,1,2])
net = Network(G,neuron,S,L1_mon,w_mon, spike_mon)
for iter1 in range(iterations):
    index = np.random.randint(10)  # index for the active neuron
    s.append(index)
    print("index",index)
    y = np.array(attributes[index][2])
    indicess, firing_t = encoding_layer(y,Imin, Imax, dimension, 100, gamma , nGRF = nGRFcells)
    net.run(100 * ms)
    G.set_spikes(indicess, firing_t * ms + 100 * (iter1 + 1) * ms)
# Create a figure
plt.figure(figsize=(40, 25))

# Create the first subplot (1 row, 2 columns, 1st subplot)
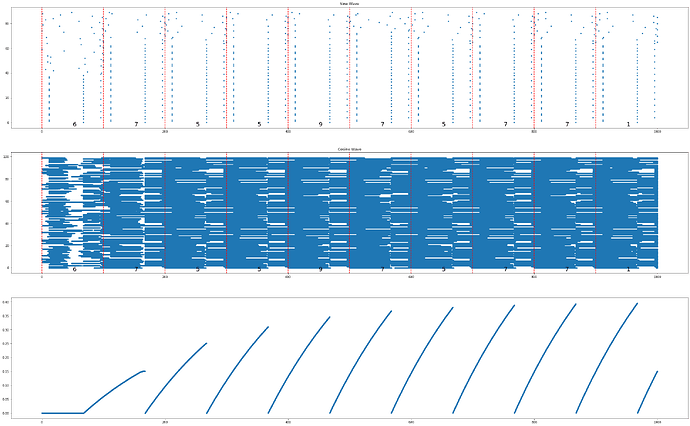
plt.subplot(3, 1, 1)
plt.plot(spike_mon.t/ms, spike_mon.i, '.')
plt.title('Sine Wave')
for l in range(0,1000, 100):
    plt.axvline(l, ls='--', c='r')
    # add text, s to a point at (x, y) coordinate in a plot
    idx = int(l/100)
    plt.text(l+50 , -3, str(s[idx]),fontsize=20)
# Create the second subplot (1 row, 2 columns, 2nd subplot)
plt.subplot(3, 1, 2)
plt.plot(L1_mon.t/ms, L1_mon.i, '.')
plt.title('Cosine Wave')
for l in range(0,1000, 100):
    plt.axvline(l, ls='--', c='r')
    # add text, s to a point at (x, y) coordinate in a plot
    idx = int(l/100)
    plt.text(l+50 , -3, str(s[idx]),fontsize=20)
plt.subplot(3,1,3)
plt.plot(w_mon.t/ms, w_mon.w1[0]/gmax, '.')
# Adjust layout for better spacing
#plt.tight_layout()
plt.show()

What have you already tried

i have tried to use SpikeGeneratorGroup with set_spikes function in for loop, it works but it seems the weights are reinitalized every time i run the simulation within the loop.

Expected output (if relevant)

output
output2275×1406 128 KB

Actual output (if relevant)

I’m expecting Brian2 to retain the parameter values from the last run and update them without resetting them. The purpose is to run all of these sets of indices and times within one simulation a 100ms window.

Full traceback of error (if relevant)

2

Hi @Abidalrekab. Your use of SpikeGenerator.set_spikes and the general approach looks correct to me. I don’t think that Brian is reinitializing the weights, as far as I can tell, it is simulating the model correctly. If you look closely at your plot, you see that the “resets” (more on this later) of the weights are not actually at the times of your stimulus change, but within the stimulus block. The reason for the steady increases in weight together with the jumps down to zero is that you have very different pre- and post-synaptic firing rates (much higher post-synaptic rate), and that you are using an all-to-all connectivity STDP scheme. After the first pre-synaptic spike (towards the middle of your first block), each post-synaptic spike will lead to some facilitation of the synapse (pre-post pairing), then the next pre-synaptic spike will apply a large depression, since all the post-synaptic spikes that happen before contribute to the depression (post-pre pairing). The “reset-like” behaviour is due to the clipping at 0, otherwise it would go below zero. I think the best fix would be to get the post-synaptic firing rate under control. In general, STDP rules are meant for a regime where the inter-spike intervals are of an order of magnitude bigger than the time constant of your STDP window (which is ~200ms here), this is clearly not the case for your post-synaptic spikes. The all-to-all STDP rule does not deal with this situation well, if you need to keep the high post-synaptic firing rate, an alternative would be to switch to a nearest-neighbour STDP rule, which only considers adjacent spikes. In the Brian equations, this means to replace Apre += dApre by Apre = dApre (and same for Apost), i.e. instead of increasing the values for every spike, setting them to a fixed value. This makes almost no difference for low firing rates, since the trace variables are usually already back to zero before the next spike increases them again, but for high firing rates it makes a big difference.

Hope that gives you a few pointers!