Description of problem
Hello everyone! I’m trying to build a single neuron model with the Pinsky Rinzel model of 1994. Even though I’m producing graphs i cannot seem to produce spikes. I’m really hoping someone can identify the problem and point out what i should do to proceed forward.
Thank you in advance everyone
the paper for reference:
- Intrinsic and Network Rhythmogenesis in a Reduced Traub Model
for CA3 Neurons (Pinsky and Rinzel, 1994).
Also since i’m a new user i’m not allowed to put more than one embedded items so i will only attach the code and when you reproduce it you will get the plots as well
Minimal code to reproduce problem
#%%
from brian2 import *
import matplotlib.pyplot as plt
start_scope()
defaultclock.dt = 0.05 * ms
Parameters = {
'C_s': 1* uF / cm ** 2,
'C_d': 1 * uF / cm ** 2,
'I_s': 0.75 * uA/ cm ** 2,
'I_d': 0 * uA/ cm ** 2 ,
'v_s': -65*mV,
'v_d': -65*mV,
'g_Na': 30 * msiemens / cm ** 2,
'E_Na': 115 * mV,
'g_Kdr': 15 * msiemens / cm ** 2,
'E_K': -15 * mV,
'g_L': 0 * msiemens / cm ** 2, # leak
'E_L': 0 * mV,
'g_Ca': 10 * msiemens / cm ** 2,
'E_Ca': 80 * mV,
'g_Kahp': 0.8 * msiemens / cm ** 2,
'g_KC': 15 * msiemens / cm ** 2,
'g_Abeta': 0 * msiemens / cm ** 2,
'E_Abeta': -65 * mV,
'g_c': 2.1 * msiemens / cm ** 2,
'p': 0.5,
}
eqs = '''
#membrane potential
#soma:
dv_s/dt=(- ILs -INa - IK_DR + (g_c/p) * (v_d-v_s) + (I_s/p))/C_s: volt
#dendrite:
dv_d/dt = ( - ILd - ICad - IK_ahp - IK_C + (g_c/(1.0-p)) * (v_s - v_d) + I_d/(1.0-p))/C_d: volt
#-(g_Abeta * (v_d - E_Abeta))
ILs = g_L * (v_s - E_L) : amp/meter**2
INa = g_Na *m_inf*m_inf * h * (v_s - E_Na) :amp/meter**2
IK_DR = g_Kdr * n * (v_s - E_K) :amp/meter**2
ILd = g_L * (v_d - E_L) :amp/meter**2
ICad = g_Ca *s*s* (v_d - E_Ca) :amp/meter**2
IK_ahp = g_Kahp * q * (v_d - E_K) :amp/meter**2
IK_C = g_KC *c* chid * (v_d - E_K) :amp/meter**2
# [ Ca ]
I_Ca = g_Ca * s**2 * (v_d - E_Ca) : amp/meter**2
dCa/dt = ( -0.13 * (I_Ca / (uA/cm**2)) - 0.075 * Ca ) / ms : 1
# Appendix
am = 0.32*(13.1 - v_s/mV)/(exp((13.1 - v_s/mV)/4.0)-1.0) / ms : Hz
bm = 0.28*(v_s/mV - 40.1)/(exp((v_s/mV - 40.1)/5.0)-1.0) / ms : Hz
an = 0.016*(35.1 - v_s/mV)/((exp((35.1 - v_s/mV)/5.0))-1.0) / ms : Hz
bn = 0.25*exp(0.5 - 0.025 *v_s/mV)/ms: Hz
ah = 0.128*(exp(17.0 - v_s/mV)/18.0) / ms : Hz
bh = 4.0 /( 1.0 + (exp((40 - v_s/mV)/5.0)) ) / ms : Hz
a_s = 1.6/( 1.0 + (exp(-0.072*(v_d/mV - 65.0))) ) / ms : Hz
b_s = 0.02*(v_d/mV - 51.1)/(exp((v_d/mV - 51.1)/5.0) -1.0) / ms : Hz
ac = (
int(v_d <= 50*mV) *
(exp((v_d/mV - 10.0)/11.0) - exp((v_d/mV - 6.5)/27.0)) / 18.975
+ int(v_d > 50*mV) * (2.0 * exp((6.5 - v_d/mV)/27.0))
) / ms : Hz
bc = ( int(v_d <= 50*mV) * (2.0 * exp((6.5 - v_d/mV)/27.0) - exp((v_d/mV - 10.0)/11.0) - exp((v_d/mV - 6.5)/27.0))/ 18.975
+ int(v_d > 50*mV) * 0) /ms : Hz
aq = clip(0.00002*Ca, 0, 0.01)/ms: Hz
bq = 0.001/ms : Hz
chid = clip(Ca/250., 0, 1) : 1
#soma dynamics
dh/dt= ah - (ah+bh)* h: 1
dn/dt= an - (an+bn)* n: 1
# gating dynamics
ds/dt = (1-s)*a_s - s*b_s : 1
dc/dt = (1-c)*ac - c*bc : 1
dq/dt = (1-q)*aq - q*bq : 1
#soma state
m_inf = 1.0/(1.0 + exp(-(v_s/mV + 30.0)/9.0)) : 1
h_inf = 1.0/(1.0 + exp((v_s/mV + 53.0)/7.0)) : 1
# tau_h = 1.0/(exp((v_s/mV+46.0)/20.0) + exp(-(v_s/mV+238)/20.0))*ms : second
n_inf = 1.0/(1.0 + exp(-(v_s/mV + 30.0)/10.0)) : 1
# tau_n = 1.0/(exp((v_s/mV+35.0)/40.0) + exp(-(v_s/mV-40.0)/50.0))*ms : second
# dh/dt = (h_inf - h)/tau_h : 1
# dn_s/dt = (n_inf - n_s)/tau_n : 1
C_s : farad/meter**2
C_d : farad/meter**2
I_s : amp/meter**2
I_d : amp/meter**2
g_Na : siemens/meter**2
E_Na : volt
g_Kdr : siemens/meter**2
E_K : volt
g_L : siemens/meter**2
E_L : volt
g_Ca : siemens/meter**2
E_Ca : volt
g_Kahp : siemens/meter**2
g_Abeta : siemens/meter**2
E_Abeta : volt
g_c : siemens/meter**2
g_KC : siemens/meter**2
p : 1
'''
neuron = NeuronGroup(1, model=eqs ,threshold='m_inf > 0.5',reset=None, method='exponential_euler',refractory='2*ms')
neuron.set_states(Parameters)
# for name, val in Parameters.items():
# setattr(neuron, name, val)
# initials
neuron.v_s = -65 * mV
neuron.v_d = -65 * mV
neuron.h = 0.
neuron.q = 0.
neuron.n = 0.
neuron.Ca = 300.
neuron.s = 0.
neuron.c = 0.
# record & run
#M= StateMonitor(pyr_model, ['Vs','Vd','Cad','ILs',"INa",'ICad','IK_ahp','IK_C','ILd'], record=True)
M = StateMonitor(neuron, ['v_s', 'v_d', 'Ca', 'q','ILs','INa', 'IK_DR', 'ILd','ICad','IK_ahp','IK_C','I_Ca','h','n', 's','c','chid','ac','bc','ah'], record=True)
run(200 * ms)
print(neuron.g_c)
# plot
import matplotlib.pyplot as plt
figure(figsize=(12, 4))
plot(M.t/ms, M.ILd[0]/mV, label='ILd')
plot(M.t/ms, M.ICad[0]/mV, label='ICad')
plot(M.t/ms, M.IK_ahp[0]/mV, label='IK_ahp')
plot(M.t/ms, M.IK_C[0]/mV, label='IK_C')
plot(M.t/ms, M.ILs[0]/mV, label='ILs')
plot(M.t/ms, M.ILd[0]/mV, label='ILd')
plot(M.t/ms, M.INa[0]/mV, label='INa')
plot(M.t/ms, M.IK_DR[0]/mV, label='IK_DR')
legend()
xlabel('Time (ms)')
ylabel('Current (mV)')
show()
# 1. Voltage plot (choose v_s or v_d)
plt.figure(figsize=(7, 4))
plt.plot(M.t / ms, M.v_s[0] / mV, label='V_s (mV)')
#for dendrite: plt.plot(M.t/ms, M.v_d[0]/mV, label='V_d (mV)')
plt.xlabel('Time (ms)')
plt.ylabel('Voltage (mV)')
plt.title('Somatic Input')
plt.legend()
plt.tight_layout()
plt.show()
# 2. Ca and q plot (share axis, different units)
plt.figure(figsize=(7, 4))
plt.plot(M.t / ms, M.Ca[0], label='Ca (Ca units)')
# plt.plot(M.t / ms, M.q[0], label='q (AHP gating)')
plt.xlabel('Time (ms)')
plt.ylabel('Value')
plt.title('Ca and q on somatic input')
plt.legend()
plt.tight_layout()
plt.show()
plt.figure(figsize=(7, 4))
plot(M.t/ms, M.h[0]/mV, label='h')
plot(M.t/ms, M.q[0]/mV, label='q')
plot(M.t/ms, M.s[0]/mV, label='s')
plot(M.t/ms, M.n[0]/mV, label='n')
plt.xlabel('Time (ms)')
plt.ylabel('Value')
plt.legend()
plt.tight_layout()
plt.show()
plt.figure(figsize=(7, 4))
plot(M.t/ms, M.c[0]/mV, label='c')
plt.xlabel('Time (ms)')
plt.ylabel('Value')
plt.legend()
plt.tight_layout()
plt.show()
plt.figure(figsize=(7, 4))
plot(M.v_d[0]/mV, M.ac[0], label='ac')
plot(M.v_d[0]/mV, M.bc[0], label='bc')
plt.xlabel('voltage)')
plt.ylabel('value')
plt.legend()
plt.tight_layout()
plt.show()
plt.figure(figsize=(7, 4))
plot(M.Ca[0], M.chid[0], label='chid')
plt.xlabel('Value')
plt.ylabel('Ca')
plt.legend()
plt.tight_layout()
plt.show()
plt.figure(figsize=(7, 4))
plot(M.v_s[0]/mV, M.ah[0], label='ah')
plt.xlabel('voltage')
plt.ylabel('value')
plt.legend()
plt.tight_layout()
plt.show()
What you have aready tried
So I’ve tried to plot several values to identify the problem.
Expected output (if relevant)
the expected output is figure 2 page 8 from the paper
Actual output (if relevant)
figures about somatic voltage , Ca and q
Full traceback of error (if relevant)
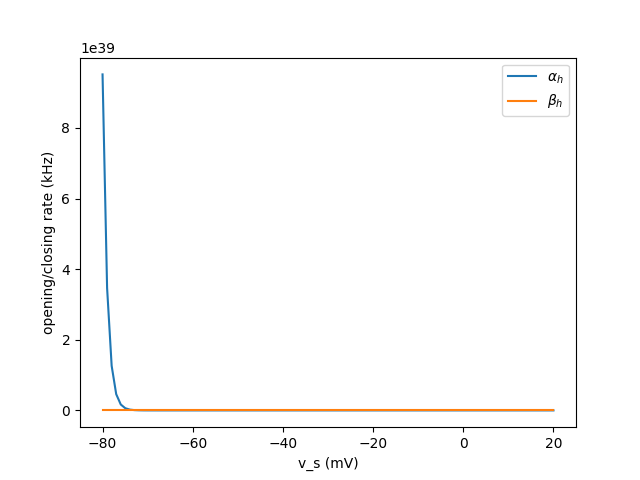
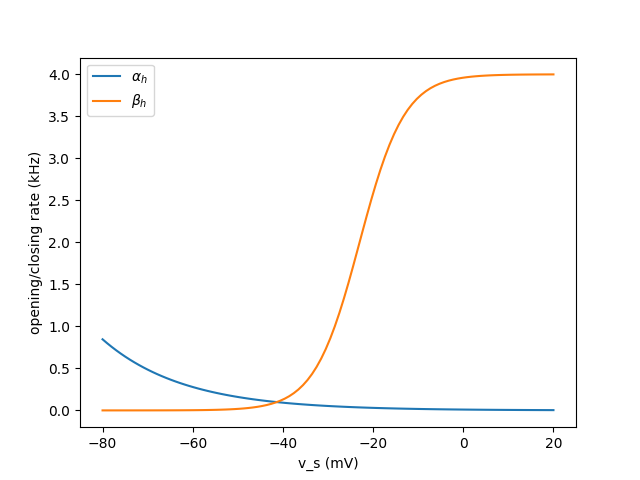
From what I’ve plotted i believe that the problem is isolated to (ac),( bc) or potentialy (ah). Could be wrong tho ![]()